# Линейная алгебра
# Вектор
Машинное обучение от простейшей линейной регрессии до сверточных нейронных сетей строится на линейной алгебре, работе с матрицами и векторами.
Изображение или текст можно перевести в вектор и произвести над ним различные преобразования, например, научить модель распознавать, кто изображен на картинке или какой окрас имеет текст комментария.
В нейронных сетях матрицами устанавливаются параметры, необходимые для преобразования слоев с информацией в процессе вычисления.
В данной статье мы рассмотрим теорию и практиктическое применение векторов. Код написан на языке python с использованием библиотеки numpy. Информация будет полезна всем, кто делает первые шаги в ml и data science.
# Скаляр
Линейная алгебра строится вокруг работы с массивами данных. Массив (англ. Array) - особая последовательность элементов, которая состоит из отдельных единиц - вещественных, натуральных или комплексных чисел. Все элементы массива должны принадлежать к одному типу данных.
В учебниках можно встретить термин скаляр, который служит для описания структурной единицы, описывающей поле вектора. Скаляры служат координатами точек в пространстве.Изображается скаляр буквой латинского или греческого алфавита. Следующая формула говорит о том, что скаляр S принадлежит множеству вещественных чисел.
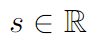
Все необходимые математические символы и определения можно посмотреть здесь
От структурных единиц перейдем к более сложным образованиям.
# Определение вектора
Вектор - упорядоченная последовательность скаляров. Векторы могут быть любой длины, но всегда одномерны - одну строку в записи. Стуктурами следующих порядков являются матрицы (двухмерные) и тензоры(n-мерные). Информацию о них вы найдете в следующих статьях.
Каждый элемент вектора имеет индекс, представлен цифрой возде каждого элемента на рисунке ниже.
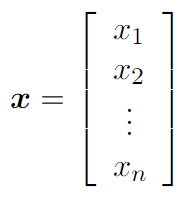
В начале пути машинного обучения, будьте готовы к тому, что один и тот же термин в разных источниках может быть описан различными словами. Например, вектором могут быть - массив, кортеж, последовательность. Вы быстро сможете привыкнуть к такому разбросу слов, однако, на первых этапах может быть некоторая путаница.
В машинном обучении векторы применяются, например, для описания состояния целевой переменой при обучении алгоритма. То есть, если мы изучаем 5 студентов и объем их курсового проекта в страницах, то вектор целевого признака будет иметь следующий вид:
y = [200, 325, 185, 220, 483]

Рисунок повторяет иллюстрацию из школьного учебника. Учитель говорил нам, что вектор - это направленный отрезок, имеющий начало и конец.
Перед нами вектор с началом в точке A и концом в точке B. Его можно так же представить как вектор
. Сразу напомним, что вектора, проложенные между двумя точками но в разных направлениях не равны друг другу, то есть:
. Данное условие будет работать с матрицами и тензорами.
Длина вектора - длина отрезка AB, при написании обозначается, как математический модуль |AB|.
Существует нулевой вектор - это точка на плоскости, .
Забегая немного вперед, приведем пример из работы с текстом, просто для иллюстрации, пока не забивайте им голову.
После преобразования слов в вектора, можно выявить закономерность, что, условно, расстояние (вектор) между слова "king" и "queen" равно расстоянию (вектору) между словами "man" и "woman" и между словами "uncle" и "aunt". Это свойство помогает математической модели понять, как соотносятся слова в этих парах. И, например, что во множесвенном числе данных слов будут действовать так же вектора одной длины.

В аналитической геометрии вы можете встретиться с понятием свободный вектор. Такой вектор не привязан к определенной точке, а просто обозначет направленный отрезок определенной длины. Такой вектор можно приложить к любой точке в пространстве. Речь в статье будет идти именно про такие векторы. Про несвободные векторы можно прочитать здесь.
Думаю, мы поняли, что же такое векторы и для чего они нужны. Время перейти к работе с веторами. В данном разделе мы соединим теорию и практикический код на python, чтобы вся информация была у вас в одном месте.
Первое, что нам необходимо сделать, импортировать numpy - базовую библиотеку для задач по линейной алгебре.
import numpy as np